100년동안 수학계에서 풀지 못했던 푸앵카레의 추측에 대해서 아시나요?
2000년 한 수학연구소에서 세계 7대 난제를 정하고 상금을 정합니다 100만달러..
그런데 불과 3년만에 100년동안 수학계를 힘들게 했던 난제를
러시아 수학자가 그 중 한문제를 풀어냅니다.
그 수학자의 이름은 그레고리 페렐만...
그리고 상금을 정중하게 거부합니다..
왜 상금을 거절하냐는 말에..
이 연구소는 19세기 한 수학자의 이름을 따서 만든 연구소입니다.
바로 앙리 푸앵카레. 페렐만이 풀었던 문제를 낸 사람입니다.
여기있는 소장도 유명한사람 입니다.
수학계의 노벨상 필즈상 수상자이죠.
소장의 이름은 세드릭 빌라니
이제부터 그 유명한 난제... 푸앵카레의 추측에 대해서 설명드리겠습니다.
이게 뭔 소릴까요...;;
좀 쉽게 말하면..
이 3차원의 구를 다른모양으로 변형시킬수 있을까??
이게바로 푸앵카레의 추측입니다.
그림으로 바꿔보면...
만약 지구로 부터 출발한 우주선에 줄을 매달고 출발한다면
우주선이 다시 지구로 왔을 때,
[줄을 당겼을때 줄이 어디에 걸리지않고 하나로 돌아오면 우주는 구의 모양일것이다]
푸앵카레의 추측은 여기서 부터 출발합니다.

앙리 푸앵카레는 당대 가장 뛰어난 수학자였습니다.
어떤문제는 증명없이 바로 결론에 이르는 뛰어난 직관을 가지고 있었습니다.
그의 추측도 증명없이던진 그냥 질문이였죠.
그리고 그의 논문끝에 이런말을 남겼습니다.
"하지만 이 질문은 우리를 너무 먼곳으로 이끌것이다"
푸앵카레는 우주의 모양이 어떻게 생겼는지 알고싶었죠.
책상위에서 우주의 모양을 추측했습니다.
우주는 우리가 사는 지구에서는 볼수없지만, 비눗방울의 모양은 볼수있듯이...
둥근 비눗방울 이것이 푸앵카레의 추측을 이해할수있는 단서가 될겁니다.
역 이름이 적혀있는 지하철 노선도.
실제 지형과는 다르지 그래도 우리는 이 지도만으로 목적지까지 갈수있습니다.
별거아닌거같지만 이것도 한 수학자 덕분이죠
그가살던시대는 18세기 그를만나러 가보면..
바로.. 페르마의 정리, 리만가설에도 나왔던 오일러입니다.
이 아름다운 도시 한가운데에는 강이있고그리고 이강에는 7개의 다리가있는데
어느 시민이 수수께끼를 내게 됩니다.
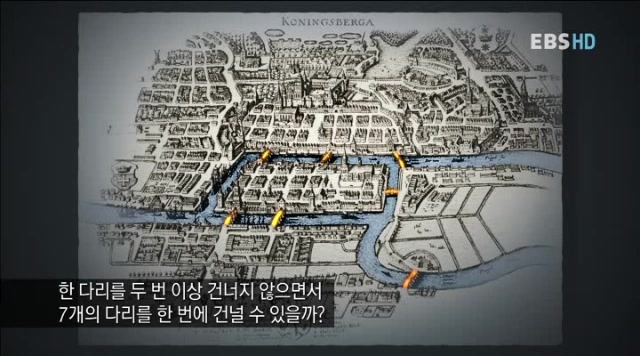
한다리를 두번이상 건너지 않으면서 7개의 다리를 한번에 건널수 있을까?

천재 수학자는 이 수수께끼의 답도 찾지 못했습니다.
이유는 답이 없었기 때문이였죠..
오일러는 어떻게 알았을까요.
오일러는 지도를 간략하게 만들었습니다.
다리는 선으로,다리를 잇는 땅은 점으로 만들었습니다.
문제가 선명해졌죠. 오일러는 여기서 한붓그리기 법칙을 찾아냈습니다.
그리고 법칙을 찾아냈습니다.

오일러의 눈으로 이 컵과 공을 한번 보면,
저 두개의 컵은 크기는 다르지만 본질은 같죠.
변형을 통해 크기를 변형하여 같게할 수 있는 것 입니다.
물체를 늘리거나 줄여도 본질은 변하지 않습니다.

하지만 잘라버리거나 구멍을내면 그 본질은 달라집니다.
공을 아무리 변형해도 절대 컵이 될수없다는 소리죠.
둘은 완전히 다른물체가 됩니다.
왜냐하면 컵에는 구멍이있지만 공에는 구멍이없기 때문이죠.
오일러덕분에 우리는 구멍이 없다는것과
다른 모양의 우주로 변형한다는것을 알수있게 되었습니다.
우리는 수학적으로 수많은 차원속에 살고있습니다.
차원은 위치를 나타내는 수가 몇개인가에 따라 나뉘어집니다.

엘리베이터안의 버튼.
한개의 숫자로 위치가 정해져. 바로 1차원입니다.
5라는 숫자 하나로 우리는 원하는 층에 갈수있죠.

선위의 모든위치는 하나의 숫자로 나타낼 수 있습니다.
그래서 선은 1차원입니다.

반면에 지구의 표면은 2차원입니다.
우리가 서있는 이위치는 동경131도 북위37도 , 독도...
131,37 단 두개의 숫자로 우리가 어디에있는지 설명할수있습니다.
만약에 100개의 숫자로 위치가 정해지는곳이있다면 그곳은 100차원일겁니다..
그렇다면 2차원은 어떤모양일까요

평평하죠.. 하지만, 다 이렇게 생겼을까요?
혹시 다르게 생긴 2차원은 없을까요?

세계지도의 끝까지 걸어가보면,
여기서 한발 더 나아가면 어떻게 될까요?

반대쪽으로 나오게됩니다. 지구는 둥그니까요
우리는 지구의 어떤지점에서 출발을하든 처음 출발한지점으로 돌아올수있습니다.
우리는 둥근모양의 지구에 살고있으니까요

배를 따라가 보면,
2차원이니 배는 다시 돌아오겠죠?

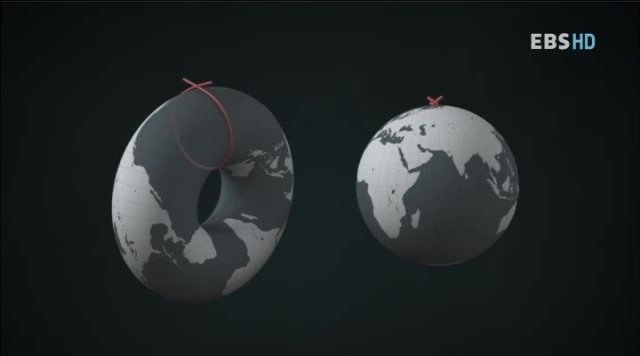
만약 지구가 이런 도넛모양이라도 가능합니다.
하지만, 같은 차원이지만 지구와 도넛모양은 본질이 다릅니다
배에 밧줄을 달고 출발한후 다시돌아왔을때 밧줄을 당겨보면,

이렇게 한점으로모이면 구 입니다.

반면 도넛은 중간에 걸립니다.
푸앵카레의 추측은 미지의 세계를 알고싶어하는 우리 본능을 자극합니다.
옛날 사람들이 끝을알수없는 바다로 나갔던것처럼 우리도 우주로 가고싶어하죠.
푸앵카레는 가보지도않은 우주를 추측했습니다.
같은 차원을 기준으로

우주가 닫힌공간이면 로켓은 다시 지구로 돌아오게 되겠죠.
마치 세계지도의 반대쪽으로 나온것처럼요

이제 줄을당겨보면 한점으로 모일겁니다.
우주는 구멍이 없는 3차원의 구라는것을 알수있습니다.

푸엥카레의 추측은 리치 흐름 정리라고도 하며, 좀 조악하게 말하자면
닫힌 3차원 공간내에 있는 모든 폐곡선이 하나의 점으로 수축될 수 있다면
그 공간은 원구(圓毬)와 위상동형일 것이라는 가설입니다
그러나 수학적인 정밀한 이해가 우리의 관심은 아니므로,
최대한 단순화시켜서 설명해도 문제의 본질을 이해하는 데는 무리가 없을 겁니다.
이날 페렐만의 강의를 듣기위해 강의실은 붐볐습니다.
수학사상 가장 어려운 문제라는 푸앵카레 추측을 나온지 20년밖에안된 방정식으로 증명해냈습니다.
그는 자신의 논문을 인터넷 웹사이트에 올려놨습니다. 상식을 깬 행동이였습니다.

언론사의 인터뷰도 모두 거절하고 최고대학 임용도 거절하고 100만달러도 거절하고,
홀연히 고향으로 돌아갔습니다.
증명에 대해서
수학적인 부분을 빼내고 간략하게 말하면,
1.
동그라미부터 출발합니다.
여기 원이 있다. 원은 1차원 선으로 되어 있으며 이렇게 정의됩니다
"2차원 평면상의 한 점으로부터 동일한 거리에 있는 점들의 집합"
쉽게 말하면 원 중심이 있고 반지름만큼 떨어져있는 모든 점을 이으면
동그라미가 된다는 뜻이다. 동그라미의 끝이 있을까 없을까 ?
그 질문은 무의미하다. 모든 점이 시작이며, 끝이니까.
2.
다음에는 지구의 표면, 보헤미안의 구슬처럼
굴곡이 없는 완벽한 구면을 생각해본니다.
구면은 2차원 곡면으로 되어 있으며 이렇게 정의된다.
"3차원 공간상의 한 점으로부터 동일한 거리에 있는 점들의 집합"
다시 말해 지구의 중심에서 모든 방향으로 반지름만큼 떨어진 점을 연결하면
지구의 표면, 즉 2차원 곡면이 된다는 것 입니다
3.
그렇다면 우리가 살고 있는 3차원 공간은 어떤 모양일까 ?
위의 1, 2로부터 유추해보면 다음과 같은 추측이 가능합니다.
"4차원 공간상의 한 점으로부터 동일한 거리에 있는 점들의 집합"이
우리가 살고 있는 3차원 우주의 모습인 것 입니다.
휘어진 선(동그라미), 휘어진 면(지구표면)처럼 우리가 사는 우주는
'휘어진 공간(곡공)'이다. 그리고 원이나 구면에 시작과 끝이 없는 것처럼,
우리 우주도 "유한하지만 끝이 없는 휘어진 공간"으로 존재하죠.
(수학적으로 말하면, 이는 '경계가 없는 3차원 다양체'를 의미하며
3차원 구면과 위상동형이다)
그러므로 그 공간의 모든 점은 시작이며 끝입니다
아마 그 모습을 직관적으로 머리에 그려볼 수 있는 사람은 많지 않을 것입니다.
그러나, 위 증명된 사실에 대하여 오래 사유해보세요. 그러면
4차원 우주의 한 점을 중심으로 펼쳐져 있는 우리 우주의 모양을
당신도 상상할 수 있을 것 입니다
부기 : 같은 뜻을 좀 다르게 설명하자면
모든 차원은, 그 차원보다 한 차원 작은 구면이 존재합니다.
2차원 평면은 1차원 구면, 즉 원을 가지며
3차원 공간은 2차원 구면, 즉 지구의 표면같은 곡면을 가지죠.
이런 식의 확대는 계속 가능합니다
수학적으로 계산해보면, 11차원이라고 생각되는 우리 우주는
12차원 공간에 한 점을 중심으로한 11차원 구면, 즉
경계가 없는 11차원 다양체가 됩니다.